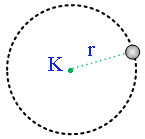
 Δίσκος
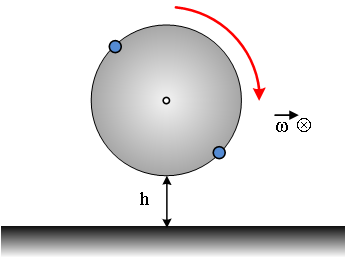
έχει το άξονα του στερεωμένο σε κατακόρυφο τοίχο έτσι ώστε το κατώτερο σημείο
της τροχιάς του να βρίσκεται σε ύψος h
= 0,8 m, από το έδαφος. Στην περιφέρεια του δίσκου και σε
δύο αντιδιαμετρικά σημεία στερεώνουμε δύο μικρά κομμάτια στόκο μάζας m
= 0,1 kg. Στρέφουμε το δίσκο με σταθερή γωνιακή ταχύτητα
σύμφωνα με την φορά περιστροφής του ρολογιού και κάποια στιγμή t0
= 0, οι δύο στόκοι αποκολλούνται ταυτόχρονα εκτελώντας οριζόντια βολή. Φτάνοντας
στο έδαφος οι δύο στόκοι κολλάνε στο σημείο επαφής χωρίς αναπήδηση. Ο στόκος που
έκανε οριζόντια βολή από το χαμηλότερο σημείο, με την πτώση έχει απώλεια στην
ενέργεια του 5,8 J, ενώ τα σημεία που "χτυπάνε" οι δύο
στόκοι στο έδαφος απέχουν μεταξύ τους απόσταση sολ
= 12 m.
Δίσκος
έχει το άξονα του στερεωμένο σε κατακόρυφο τοίχο έτσι ώστε το κατώτερο σημείο
της τροχιάς του να βρίσκεται σε ύψος h
= 0,8 m, από το έδαφος. Στην περιφέρεια του δίσκου και σε
δύο αντιδιαμετρικά σημεία στερεώνουμε δύο μικρά κομμάτια στόκο μάζας m
= 0,1 kg. Στρέφουμε το δίσκο με σταθερή γωνιακή ταχύτητα
σύμφωνα με την φορά περιστροφής του ρολογιού και κάποια στιγμή t0
= 0, οι δύο στόκοι αποκολλούνται ταυτόχρονα εκτελώντας οριζόντια βολή. Φτάνοντας
στο έδαφος οι δύο στόκοι κολλάνε στο σημείο επαφής χωρίς αναπήδηση. Ο στόκος που
έκανε οριζόντια βολή από το χαμηλότερο σημείο, με την πτώση έχει απώλεια στην
ενέργεια του 5,8 J, ενώ τα σημεία που "χτυπάνε" οι δύο
στόκοι στο έδαφος απέχουν μεταξύ τους απόσταση sολ
= 12 m.
α. Να σχεδιάσετε
τον δίσκο την στιγμή t0
που αποκολλούνται οι στόκοι και να αιτιολογήσετε την μορφή που σχεδιάσατε.


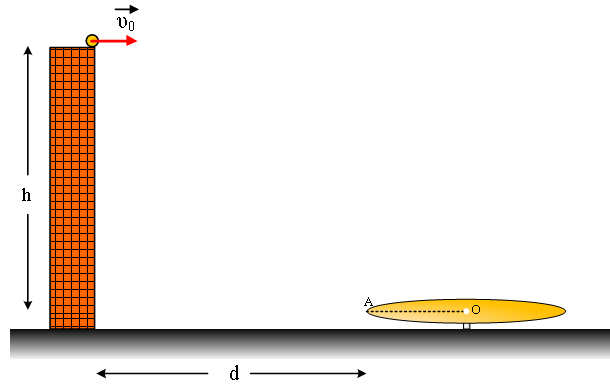 Από
κτήριο ύψος
Από
κτήριο ύψος 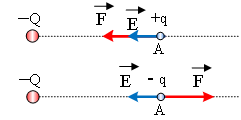 ΗΛΕΚΤΡΙΚΟ
ΠΕΔΙΟ
ΗΛΕΚΤΡΙΚΟ
ΠΕΔΙΟ

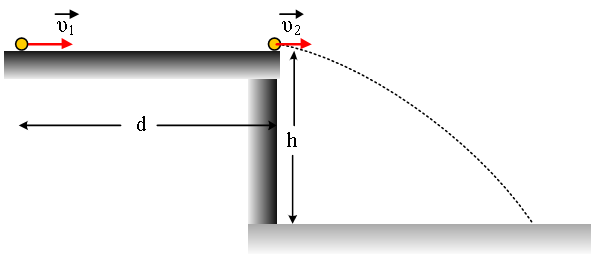 Εκτοξεύουμε
την χρονική στιγμή
Εκτοξεύουμε
την χρονική στιγμή  Ένα βομβαρδιστικό
αεροπλάνο πετά σε ύψος
Ένα βομβαρδιστικό
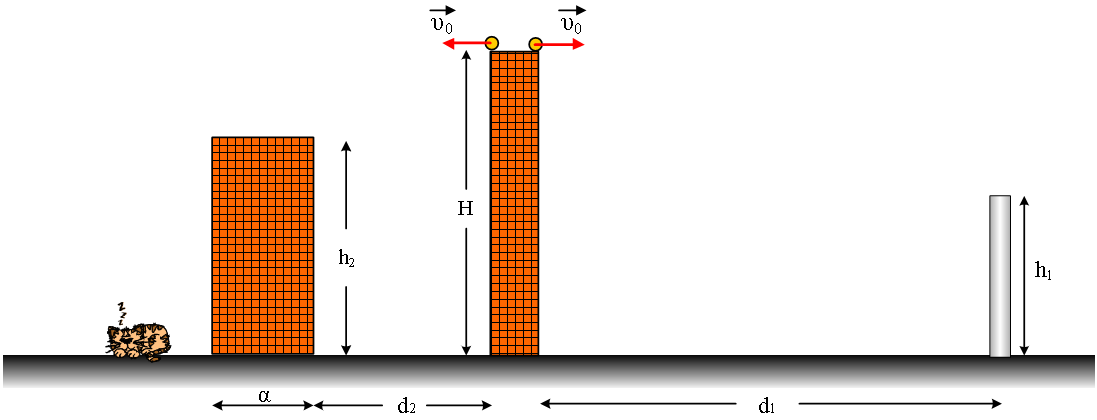
αεροπλάνο πετά σε ύψος  Ένας
άνθρωπος έχει βγάλει βόλτα για παιχνίδι το σκύλο του, ύψους
Ένας
άνθρωπος έχει βγάλει βόλτα για παιχνίδι το σκύλο του, ύψους 
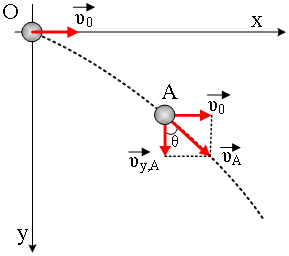 Ένα σώμα μάζας
Ένα σώμα μάζας