Μια μικρή φορτισμένη σφαίρα, μάζας
m=10g και φορτίου q1, ηρεμεί στο κάτω άκρο ενός κατακόρυφου νήματος
(θέση Α) μήκους ℓ=1m από μονωτικό υλικό. Φέρνουμε στο σημείο Ο, το οποίο απέχει
κατακόρυφη απόσταση h=0,2m και οριζόντια
απόσταση (ΟΓ)=1m από την θέση Α, ένα σημειακό φορτίο q2=4μC, με αποτέλεσμα
η σφαίρα να εκτρέπεται και τελικά να ισορροπεί στη θέση Β, μεταξύ του Ο και του
Γ.
i) Να βρεθεί η
γωνία εκτροπής του νήματος στην τελική θέση ισορροπίας της σφαίρας.
ii) Να
υπολογιστούν η οριζόντια και η κατακόρυφη συνιστώσα της τάσης του νήματος στην
τελική θέση.
iii) Να βρεθεί το φορτίο q1 της σφαίρας.
iv) Κατά τη διάρκεια της μετακίνησης της σφαίρας από
τη θέση Α στη θέση Β, το έργο της δύναμης που δέχτηκε από το ηλεκτρικό πεδίο είναι
θετικό, αρνητικό ή μηδέν; Να δικαιολογήσετε την απάντησή σας.
Δίνεται η σταθερά του νόμου Coulomb k=9∙109Ν∙m2/C2
και g=10m/s2.


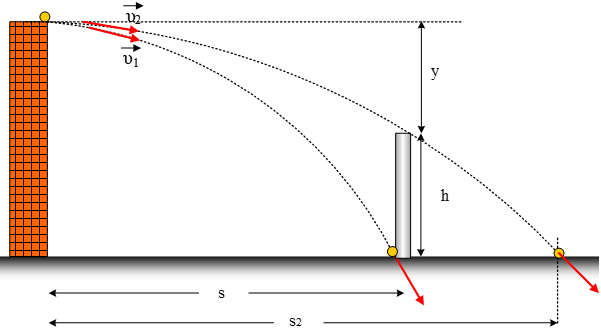 Διαθέτουμε
μία μηχανή που εκτοξεύει μικρά μπαλάκια και βρισκόμαστε στην ταράτσα μιας
πολυκατοικίας ύψους Η. Απέναντι από την πολυκατοικία βρίσκεται μία κολόνα της
ΔΕΗ ύψους
Διαθέτουμε
μία μηχανή που εκτοξεύει μικρά μπαλάκια και βρισκόμαστε στην ταράτσα μιας
πολυκατοικίας ύψους Η. Απέναντι από την πολυκατοικία βρίσκεται μία κολόνα της
ΔΕΗ ύψους 


